Уровни коррекции Фибоначчи. Как их использовать?

Уровни коррекции Фибоначчи. Звучит сложно, не так ли? Для чего они нужны? И как они работают?

К счастью для трейдеров, уровни коррекции Фибоначчи - это нечто большее, чем просто красивое слово. Фактически, это название инструмента, используемого для прогнозирования потенциальных уровней поддержки и сопротивления.

Во-первых, давайте познакомимся с самим Фибоначчи, а затем уже разберемся, как изобретенная им концепция помогает в крипто трейдинге.

Зависимости чисел Фибоначчи встречаются буквально на каждом шагу

Леонардо Пизанский (известный как Фибоначчи) - средневековый математик, представивший миру уникальную последовательность чисел, известную сегодня как «последовательность Фибоначчи»:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584... (и так до бесконечности)

Каждое число в последовательности получается из суммы двух предыдущих чисел. Интересно, не так ли? Но это было бы слишком просто. Каждое число примерно в 1,618 раз больше, чем предыдущее (и наоборот, меньшее число составляет 0,618 от большего, начиная с четвертого члена ряда). Это так называемое «золотое соотношение» или «число фи», которое невероятным образом проявляется в каждом элементе природы.

Возьмем, например, цветы: у лилий 3 лепестка, у лютиков 5, у цветков цикория 21, а у ромашек 34 и так далее. Интересно, что эти цифры соответствуют последовательности Фибоначчи, и даже при расположении лепестков «учитывается» цифра 0,618 для оптимального взаимодействия растения с солнечным светом и другими жизненно важными факторами.

Примеры последовательности Фибоначчи в природе бесконечны. Теперь мы даже можем говорить о крипто трейдинге, когда упоминаем великого математика.

В частности, трейдер может высчитать уровни (которые, вероятнее всего, очень важны для цены актива), разделяя верхнюю и нижнюю точку тренда (или наоброт) по «золотому сечению» и другим соотношениям в последовательности. Важными коэффициентами являются:

• 0,382 –отношение любого числа в последовательности к числу, расположенному через одно справа.
• 0,236 – число, полученное путем деления одного из чисел на число, расположенное через два справа.

Как вы потом убедитесь, цена регулярно проявляет зависимость от этих уровней. Это помогает трейдеру в выборе оптимальных точек входа и выхода, так же как обеспечивает цветку оптимальную структуру для поглощения солнечного света.

Поиск уровней поддержки Фибоначчи

Прежде чем использовать этот инструмент для определения потенциальных уровней поддержки или сопротивления, трейдеру необходимо определить «максимум колебания тренда» и «минимум колебания тренда» (верхняя и нижняя точка коррекции или отката).

Максимум тренда - это свеча на пике тренда на любом таймфрейме, справа и слева от которой расположены более низкие максимумы. И наоборот, минимум тренда - это нижняя свеча, справа и слева от которой расположены более высокие минимумы.

Как только вы идентифицировали эти точки, выбирайте на используемой вами платформе инструмент Фибоначчи и соединяйте минимум с максимумом. Платформа автоматически сформирует вам потенциальные уровни поддержки (уровни коррекции Фибоначчи).

Каждый уровень коррекции Фибоначчи высчитывается путем разделения области между максимумом и минимумом тренда согласно важным коэффициентам соотношения последовательности Фибоначчи.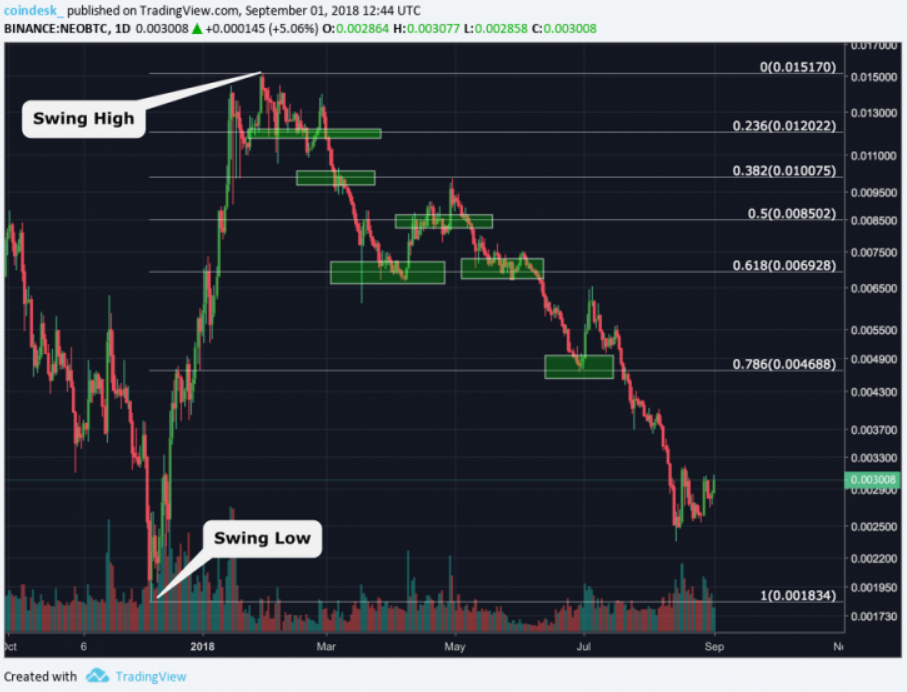

На приведенном выше графике минимум тренда NEO (NEO / BTC) 0,001834/BTC был соотнесен к максимуму тренда 0,015170/BTC при помощи инструмента «Уровни Фибоначчи».

Как вы можете видеть, уровни 0.236, 0.382, 0.5, 0.618, 0.786 выступали (по крайней мере, на какое-то время) в качестве поддержки на всем пути последующего падения цены актива.

Если трейдер воспользовался этим инструментом, то он мог бы предположить, в каких точках цена получит поддержку, прежде чем сделать следующий шаг. Таким образом можно было определять идеальные точки входа или выхода.

Поиск уровней сопротивления Фибоначчи

По своей сути, процесс поиска потенциальных уровней сопротивления такой же, за исключением того, что на этот раз вы будете соединять максимум тренда к минимуму.

И вновь благодаря соотношениям в последовательности Фибоначчи будут построены уровни коррекции.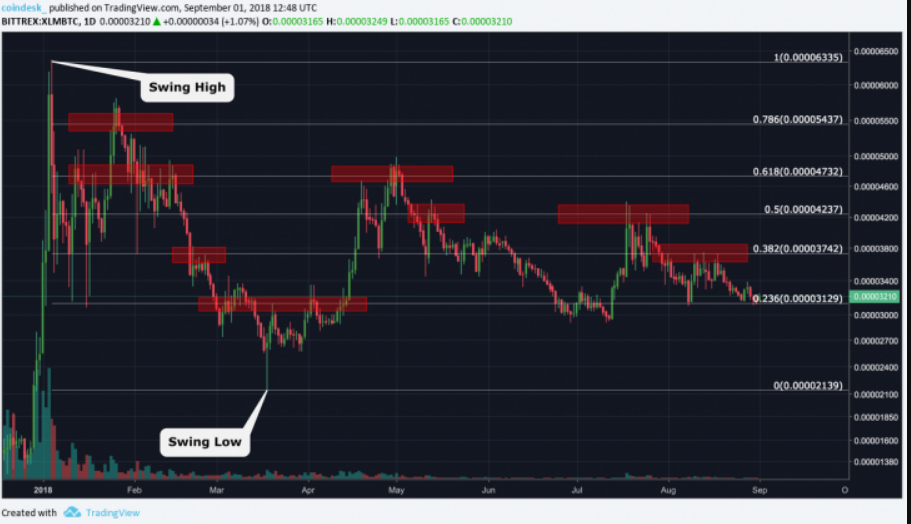

На приведенном выше графике ожидаемые уровни сопротивления Stellar Lumens (XLM / BTC) были получены после соединения максимума 0,00006335/BTC к минимуму 0,00002139/BTC.

Далее, как и утверждает теория, цена «обращала внимание» на эти уровни.

Таким образом, уровни 0.786, 0.618, 0.5 и 0.382 обеспечивали сопротивление, что позволяло трейдеру определить оптимальные целевые точки относительно своей позиции для получения прибыли.

Вывод

Важно помнить, что данный инструмент может быть полезен при определении возможных уровней поддержки и сопротивления, но, как и любой другой инструмент технического анализа, он не гарантирует вам положительного результата. Чтобы повысить вероятность верного определения важных уровней коррекции, необходимо использовать этот инструмент вместе с другими индикаторами, такими как скользящие средние или индекс относительной силы (RSI).

Например, если скользящая средняя находится в той же области, что и уровень коррекции Фибоначчи, то цена, скорее всего, отреагирует на него (так как два объединенные уровня сопротивления или поддержки более значимы, чем один).

Если вы пересчитывали каждое соотношение в последовательности приведенных выше чисел, то, возможно, заметили, что коэффициент 0.5 получить таким способом невозможно, однако он отображается как важный в инструменте определения уровней коррекции Фибоначчи. Уровень 0.5 включен в расчеты трейдинговых платформ, потому что практика показывает, что цена очень часто реагирует на него как с точки зрения поддержки, так и сопротивления.

Хотите зарабатывать на крипте? Подписывайтесь на наши Telegram каналы!